TOXICOLOGIE

Les idées reçues sont étonnamment solides. Il faut beaucoup d'insistance pour en venir à bout... :

CRITÈRES D'INTERPRÉTATION DIAGNOSTIQUE EN TOXICOLOGIE

Les ressources indispensables

Pour introduire le sujet:

                    par Hugues Rousset, Denis Vital Durand, Jean-Louis Dupond, et Michel Pavic

                    (et les deux éditions antérieures)

Pour comprendre en français sur Wikipedia le théorème de Bayes et ses conséquences avant de se reporter aux sites en anglais :

Pour comprendre en anglais sur Wikipedia les valeurs prédictives :

Pour approfondir en anglais sur Wikipedia les courbes ROC :

Le laboratoire est spécialisé dans la recherche des médicaments et des stupéfiants dans les liquides biologiques en CPG-SM

L'essentiel du travail de ces auteurs a consisté à montrer qu'il valait mieux utiliser des fréquences au lieu des probabilités correspondantes si on voulait être compris du plus grand nombre c'est à dire surtout les étudiants, les médecins, les magistrats etc.

Finalement, il n'y a plus qu'une loi et un théorème à retenir pour comprendre le raisonnement qui mène à une interprétation diagnostique

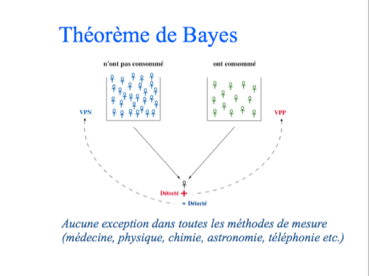
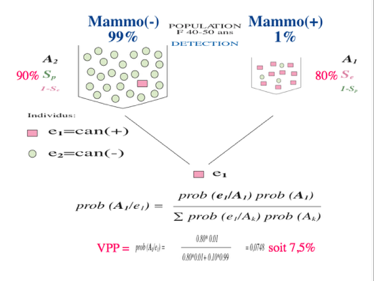
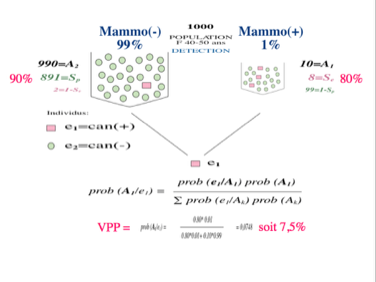
En prenant l'exemple le plus répandu très bien connu de la mammographie, 75% des médecins ont fait un diagnostic erroné de cancer du sein formulé en termes de probabilités

Le même problème est mieux compris par les médecins si on le leur présente en termes de fréquences équivalentes

La même expérience a été conduite à partir de l'exemple aussi répandu et très bien connu des empreintes génétiques où 99% des étudiants en droit ont fait un diagnostic erroné de culpabilité formulé en termes de probabilités

Le même problème a été mieux compris par les étudiants en droit en le leur présentant en termes de fréquences équivalentes

Les scientifiques ont compris depuis longtemps que l'exigence de preuve devait intégrer le doute que recouvre la mesure de la part du non spécifique dans la mesure totale

En médecine, les difficultés surgissent quand l'existence du non spécifique est niée et qu'on sacralise la sensibilité au détriment de la spécificité

Tout médecin sait que l'interprétation diagnostique s'obtient par accumulation de signes cliniques et non cliniques et qu'un signe isolé fait rarement à lui seul un diagnostic binaire de type vrai/faux

Il n'y a que le théorème de Bayes qui permette d'évaluer la probabilité d'un diagnostic quelle que soit sa nature et en tant qu'hypothèse à vérifier

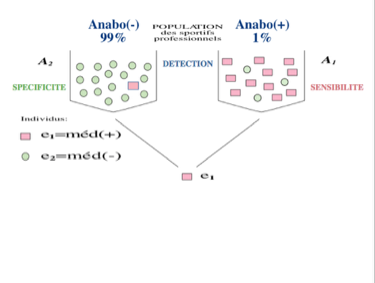
Il faut d'abord connaître la probabilité a priori (ou prévalence) dans la sous-population. Appliqué aux anabolisants, il faut savoir combien de personnes en prennent dans la sous-population dont est issue la personne testé lors d'un contrôle antidopage par exemple. Sinon, la seule connaissance de la sensibilité et de la spécificité ne sert à rien.

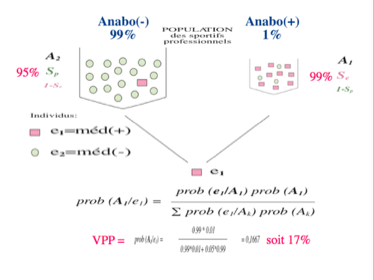
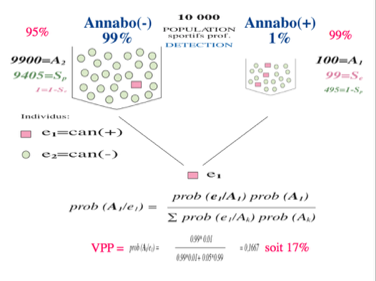
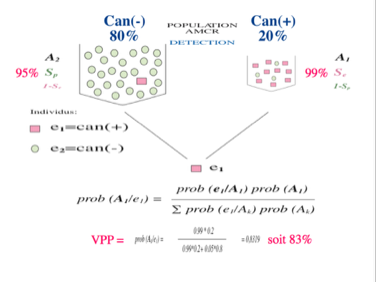
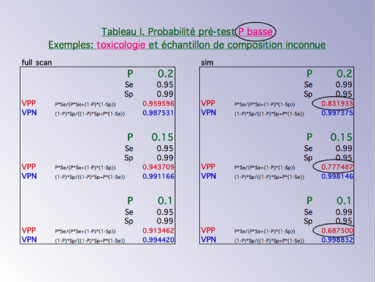
Si la prévalence est de 1%, on se rend compte qu'une spécificité de 95% et une sensibilité de 99% donnent à peine une probabilité ou Valeur Prédictive Positive (VPP) de 17% qu'un échantillon positif soit la preuve d'une consommation d'anabolisants. Pour éviter une sanction injustifiée, il faut donc augmenter la spécificité par tout moyen.

Quand le calcul est fait avec les fréquences c'est à dire à partir des dénombrements, le résultat est évidemment le même mais il est beaucoup plus compréhensible et presque évident.

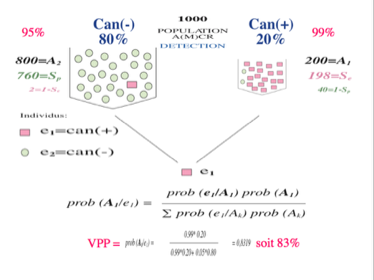
Si la prévalence est de 20% comme on peut s'y attendre pour le cannabis, on se rend compte que la même spécificité de 95% et la même sensibilité de 99% donnent une probabilité ou Valeur Prédictive Positive (VPP) de 83% qu'un échantillon positif soit la preuve d'une consommation de cannabis. Pour éviter une sanction injustifiée, il faut aussi augmenter la spécificité par tout moyen mais il est très rassurant de pouvoir partir de plus haut.

Quand le calcul est fait avec les fréquences c'est à dire à partir des dénombrements, le résultat est évidemment le même mais il est beaucoup plus compréhensible et presque évident.

On retiendra surtout que dans le cas du cannabis, l'hypothèse de consommation n'est vérifiée que pour 83 personnes sur les 100 personnes détectées positives. On sait d'ores et déjà qu'un signe isolé conduira inéluctablement à 17% d'erreurs.

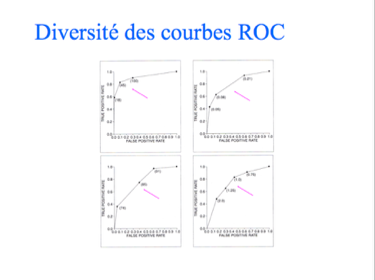
La courbe ROC est une courbe qu'on peut qualifier d'étalonnage appliquée à un radar. C'est une courbe expérimentale qui permet de trouver le meilleur couple sensibilité/spécificité. Elle permet de rappeler que la sensibilité et la spécificité sont indissociables.

En tant que courbes expérimentales, les courbes ROC peuvent prendre n'importe quelle forme. Leur détermination n'a rien d'intuitif.

Appliqué au cancer du sein de l'exemple vu plus haut dont la prévalence retenue est de 1% pour une année d'âge, on se rend compte que la spécificité de 90% et la sensibilité de 80% donnent une probabilité ou Valeur Prédictive Positive (VPP) de 7,5% qu'une mammographie soit la preuve d'un cancer du sein. Pour éviter une intervention injustifiée, il faut augmenter la spécificité par tout moyen et notamment un examen anatomo-pathologique.

Quand le calcul est fait avec les fréquences c'est à dire à partir des dénombrements, le résultat est évidemment le même mais il est beaucoup plus compréhensible et presque évident.

On sait que les autorités de santé de presque tous les pays du G8 ont imposé la prise en compte des Valeurs Prédictives Positives (VPP) et des Valeurs Prédictives Négatives (VPN) pour éviter des traitements médicaux et chirurgicaux injustifiés à la suite des campagnes de dépistage des principaux cancers (sein, colon, prostate)

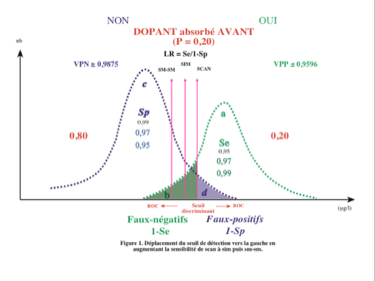
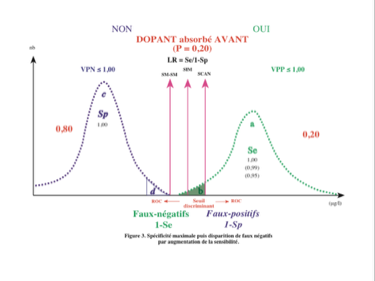
L'augmentation de la sensibilité par déplacement du seuil vers la gauche diminue le nombre des faux négatifs mais fait apparaître des faux positifs.

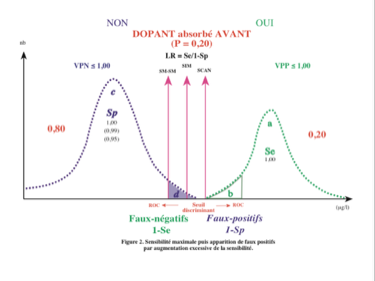
Il existe parfois un seuil de sensibilité idéal. En se déplaçant vers la gauche (meilleure sensibilité) on risque de faire apparaître inutilement des faux positifs...

... et en se déplaçant vers la droite (meilleure spécificité), on risque de faire apparaître inutilement des faux négatifs.

Il est utile de pouvoir disposer de plusieurs méthodes différant entre elles soit par un procédé chimique soit par un procédé physique. Et, c'est indispensable face à un signe isolé.

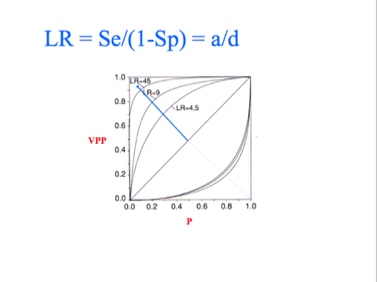
Le rapport LR exprimé en termes de sensibilité et de spécificité permet de comprendre ce que le calcul de la VPP apporte de plus que la probabilité a priori ou prévalence.

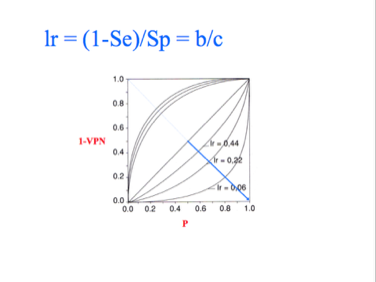
Et, inversement, le rapport lr exprimé en termes de sensibilité et de spécificité permet de comprendre ce que le calcul de la VPN apporte de plus que la probabilité a priori ou prévalence.

La pathognomonie stricto sensu n'existe pas mais en pratique il est bien utile de comprendre qu'elle correspondrait au cas très particulier d'une sensibilité de 100% et d'une spécificité de 100%.

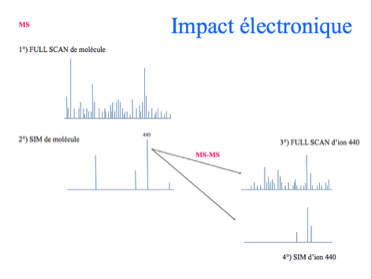
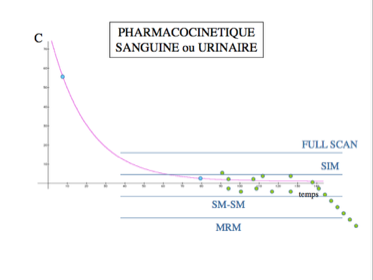
En toxicologie et dans la lutte contre le dopage, la spectrométrie de masse peut être utilisée à trois niveaux différents de sensibilité correspondant à trois procédés physiques d'acquisition des données.

L'Agence Mondiale Antidopage (AMA ou WADA) privilégie toujours à juste titre la méthode de plus grande spécificité. C'est en parfaite cohérence avec les méthodes mathématiques bayésiennes d'interprétation diagnostiques.

Les connaissances requises pour l'établissement d'un diagnostic sont peu nombreuses mais suffisamment complexes pour que le travail d'interprétation soit confié à un personnel expérimenté quand l'enjeu en vaut la peine. En médecine c'est les médecins.

Il n'y a que deux moyens d'augmenter la VPP ou probabilité que la personne ait consommé la substance recherchée (toxicologie, dopage...) quand elle est positive à un test sanguin ou urinaire: il faut augmenter la spécificité ou la prévalence ou les deux.

La détection du THC par quantification lors de la recherche d'une consommation de cannabis (lutte contre le dopage, accident de la circulation...) est l'exemple le mieux connu d'une utilisation possible de trois niveaux de sensibilité différents avec toutes les conséquences annoncées sur les faux positifs et les faux négatifs.

Les moyens de déjouer la présence d'un signe isolé avec son cortège d'incertitudes sont nombreux et efficaces. Le signe isolé à l'issue des recherches est rare. Il faut refuser de prendre une sanction face à un signe isolé c'est à dire non confirmé par d'autres informations sous peine de se tromper avec une probabilité proche de la certitude.

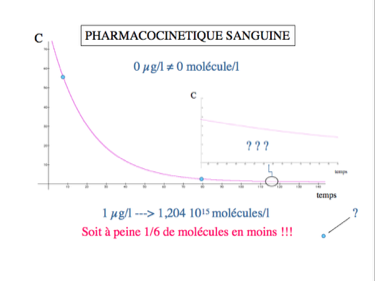
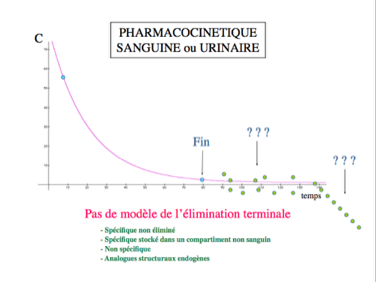
On sait grâce aux courbes pharmacocinétiques comment est éliminé du sang un sixième de la dose de substance consommée. En revanche, il n'existe pas de courbe de référence concernant l'élimination des cinq autres sixièmes. Personne ne sait donc à quel moment l'organisme n'en contient plus du tout.

Il n'existe aucun modèle de l'élimination terminale d'une substance consommée.

L'augmentation de la sensibilité peut conduire à la détection de molécules dont personne ne sait à quoi elles correspondent d'un point de vue pharmacocinétique.

L'interprétation d'un résultat et donc le diagnostic de consommation d'une substance impose de connaître la prévalence de la sous-population dont est issu le prélèvement. L'idéal est de disposer en cascade d'une sous-population, d'une sous-sous-population, d'une sous-sous-sous-population etc.

La prévalence de la consommation d'une substance donnée dans la population générale est évidemment proche de zéro. D'où la nécessité de bien circonscrire la sous-population prélevée.

La description précise d'une sous-population peut prendre plusieurs lignes voire une page !

Il faut toujours faire un tableau des VPP et VPN pour différentes valeurs de prévalence (ou probabilité à priori ou probabilité pré-test etc.). En pharmacologie, les patients sont traités et on s'attend à ce qu'ils aient pris leur traitement, la prévalence d'avoir absorbé le médicament recherché est élevé. le risque d'erreur par faux positif est faible.

En toxicologie (intoxications), face à une très faible concentration, la probabilité ou prévalence que le patient ait absorbé la substance retrouvée est faible voire très faible. Le risque d'erreur par faux positif est donc élevé.

Il est important de comprendre que plus la prévalence est faible plus le risque d'erreur par faux positif est élevé même avec une sensibilité et une spécificité très élevées.

Il ne faut pas espérer avoir très souvent une sensibilité et une spécificité proches de 100% car il s'agirait alors de pathognomonie, qui est mathématiquement très improbable. En plus, un couple 99%/99% ne met pas à l'abri non plus d'erreurs par faux positifs lors d'un signe isolé.

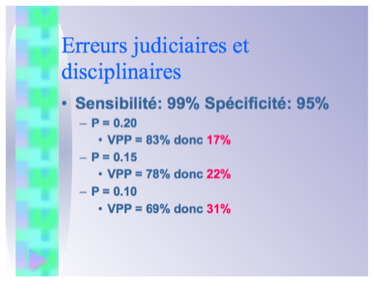
En présence d'un signe isolé, l'erreur judiciaire et l'erreur disciplinaire ont une probabilité élevée tout comme l'erreur médicale.

Une prévalence très basse peut rendre l'interprétation d'un résultat aussi aléatoire qu'un tirage au sort. C'est le cas des empreintes génétiques effectuées sur la population générale et quand le nombre des loci semblables est trop faible malgré un couple sensibilité/spécificité extrêmement élevé.

Il ne faut pas surestimer une méthode et il faut en connaître les limites sans les cacher aux autres.

Il est mathématiquement démontré et expérimentalement vérifié que c'est la méthode la plus spécifique qui fait le diagnostic. La sensibilité sert préférentiellement à la quantification d'un signal.

Le problème

Un résultat d'analyse biologique (positif ou négatif) est totalement différent de son interprétation (confirmer ou non l'hypothèse diagnostique). Un résultat d'analyse biologique relève de la certitude en classant le résultat au-dessus ou au-dessous d'une moyenne arbitraire ou d'un seuil.  L'interprétation d'un résultat renvoie à une incertitude et relève d'une probabilité. Constater une augmentation du nombre des globules rouges au-dessus d'une valeur fixée à l'avance relève de la certitude. En revanche, interpréter cette hausse comme le signe d'une anomalie sous-jacente relève d'une probabilité plus ou moins élevée en fonction de l'hypothèse diagnostique proposée. De plus, la plupart des signes biologiques peuvent correspondre à plusieurs hypothèses diagnostiques, e.g., un abaissement du taux d'hémoglobine à plusieurs anémies. Il faut faire alors une interprétation diagnostique différente pour chaque possibilité diagnostique. On retrouve la même problématique avec une image radiologique, un examen de lame en anatomo-pathologie, une empreinte génétique en biologie cellulaire, un signe à l'examen clinique etc. Et le raisonnement s'étend à tous les signes de toutes les disciplines et particulièrement à tous les résultats fournis par un appareil de mesure physique y compris en physique, chimie, astronomie, téléphonie etc. En général, on ne considère qu'une seule hypothèse. En toxicologie, cette hypothèse est toujours "consommation ou pas consommation d'un produit X".

Donc, en toxicologie comme ailleurs, on peut déclarer un résultat positif ou négatif en fonction d'un seuil de positivité moyen fixé à l'avance mais la réponse à la question "a consommé ou non ?" est plus aléatoire et oblige à recourir à un modèle d'interprétation qui renverra plus ou moins d'incertitude sous la forme d'une réponse plus ou moins probable. Ce modèle est le  (ou

et on parle d'interprétation bayésienne. Il ne prend en compte que la valeur prédictive positive () pour poser un diagnostic en présence d'un signe positif ou la valeur prédictive négative () pour le rejeter en présence d'un signe négatif.

La recherche de traces

L'interprétation diagnostique est souvent aidée par la hauteur du signal. Si la hauteur du signal est grande, en toxicologie c'est la concentration ou plus exactement la distance entre la mesure et la ligne de base, on aura tendance à se passer d'une interprétation et à confondre positivité et consommation. En revanche, si la hauteur du signal est faible, on aura tendance à s'en remettre à l'expérience de l'opérateur donc à son intuition. C'est intuitivement vrai mais mathématiquement risqué car la hauteur du signal est un paramètre parmi d'autres lors de l'interprétation et il relève plus du résultat (positif ou négatif) et moins du diagnostic (consommation ou pas consommation). En tous cas, lors de la recherche de traces donc en présence d'un signal faible, il est recommandé de renoncer à toute interprétation hâtive car le risque d'erreur est très élevé et le diagnostic n'est souvent pas plus précis qu'un tirage au sort à pile ou face.

Rester scientifique

Il y a un seul moyen de mesurer la probabilité diagnostique; c'est de faire le calcul et rester prudent. Aucune certitude n'existe et c'est la raison pour laquelle on entend souvent que la médecine est un art et pas une science. En fait, il y a un moyen de se rapprocher de la science et qui est utilisé tous les jours en médecine. Il consiste à récolter plusieurs signes de nature, d'origine et de disciplines différentes qui permettront de raisonner à l'intérieur d'une sous-population la plus restreinte possible c'est à dire correspondant le mieux à l'hypothèse diagnostique posée. On sait très bien que le diagnostic est posé si tous les signes sont réunis. Il suffit donc d'en récolter le plus possible.

Les enjeux

La question de l'interprétation se pose donc vraiment au cours de l'observation médicale tant que le diagnostic n'est pas posé puis chaque fois qu'un signe isolé est disponible ou quelques signes seulement qui ne font pas à eux seuls le diagnostic. Les enjeux de l'interprétation sont considérables au moment de prendre une décision disciplinaire dans la lutte contre le dopage ou lors de la présentation d'un résultat en toxicologie médico-légale. Si la réponse à la question posée n'est pas dans le dossier et que le toxicologue ne dispose que de ses propres résultats, il faudra rassembler des signes de nature, d'origine et de méthodes différentes pour aboutir à un résultat très probable. Ce sera par exemple plusieurs milieux biologiques, plusieurs métabolites, plusieurs techniques etc. Mais, sur un signal faible d'une seule molécule dans un seul milieu avec une seule technique, il peut devenir hardi d'interpréter un résultat qui semble se détacher de la ligne de base. La connaissance de l' aide dans tous les cas à rejeter ou confirmer une hypothèse à laquelle on tenait beaucoup.

La méthode

La méthode générale est relativement simple comme d'habitude si on laisse de côté l'historique de la démarche qui est toujours complexe comme tous les historiques. La première des choses est de connaître la probabilité du diagnostic dans la sous-population étudiée à laquelle est rattachée la personne retenue. Elle est souvent appelée "probabilité a priori" aussi bien que "". Il ne s'agit pas stricto sensu d'une probabilité mais d'une fréquence c'est à dire d'un dénombrement observable. C'est donc une valeur expérimentale. Cette probabilité varie à chaque recueil d'un signe supplémentaire puisque la sous-population s'affine à chaque addition d'un signe qu'il soit positif ou négatif.

La deuxième des choses est de connaître la  (ou ) de la méthode de mesure. La sensibilité est la probabilité du diagnostic quand le résultat est positif i.e. au-dessus d'une valeur moyenne arbitrairement fixée. On pourrait s'en satisfaire mais ça serait sans compter la spécificité qui est la probabilité de rejeter le diagnostic quand le même résultat est négatif. Comme la spécificité et la sensibilité se chevauchent, on ne peut pas tenir compte de l'une sans l'autre. Et, quand on augmente la sensibilité, on augmente automatiquement le nombre de faux positifs qui peut devenir dominant pour une sensibilité exagérée. Il faut donc fixer une valeur de référence du couple sensibilité-spécificité qui ne peut être obtenue que par le  (ou ) pour minimiser à la fois le nombre de faux négatifs et de faux positifs. Comme il ne s'agit pas d'optimiser le résultat mais d'optimiser le diagnostic, le théorème de Bayes a besoin d'une probabilité a priori sans laquelle aucune optimisation n'est possible.

Il s'agit d'un couple car l'une ne peut pas varier sans l'autre. Cette variation se fait toujours en sens inverse l'une de l'autre mais pas forcément dans les mêmes proportions. Là aussi, il ne s'agit pas de probabilités stricto sensu mais de deux fréquences c'est à dire de dénombrements observables. C'est donc aussi deux valeurs expérimentales. Elles varient en fonction des appareils, des opérateurs, des moments mais aussi du temps à partir de la dernière calibration ou de la dernière maintenance des appareils et de bien d'autres paramètres. Il s'agit donc bien de valeurs liées au moment et au lieu de l'analyse et de ce fait difficiles à connaître avec précision.

Il faut finalement disposer en tout et pour tout de trois fréquences : une probabilité a priori, une sensibilité et une spécificité. Elles sont considérées comme des probabilités et traitées par le théorème de Bayes qui est une division très ordinaire. Certes, on ne les connaît pas avec une très grande précision. Mais, en revanche, les ordres de grandeur sont connus et amplement suffisants pour faire un calcul global et prendre une décision. En médecine, la décision consiste le plus simplement du monde à demander un examen complémentaire à la recherche d'un autre signe et ainsi de suite. L'interprétation diagnostique se fait sur l'ensemble des signes recueillis à chaque étape.

La difficulté

La seule difficulté est de poser le problème correctement. Il faut s'habituer au raisonnement bayésien et devant un résultat se poser la question: "D'où vient-il ?". Ce raisonnement s'appelle l' et il est asymptotiquement égal au raisonnement statistique. Ce qui lui permet de s'affranchir de la taille des échantillons ce qui n'est pas le cas de la méthode statistique. A condition de bien maîtriser les notions de prévalence, sensibilité et spécificité sinon la pratique ne rejoindra pas la théorie.

Les courbes ROC

L'inconvénient du théorème de Bayes est qu'il est une démonstration théorique. C'est une démonstration théorique qu'on ne doit pas interpréter un résultat brut suivant la seule alternative positif-négatif et que considérer uniquement le résultat brut positif-négatif est une erreur qui conduit à des interprétations fausses donc à des diagnostics faux dans des proportions statistiquement prévisibles. Le théorème de Bayes est extrêmement utile pour l'évaluation de méthodes et la comparaison de méthodes puis l'association de méthodes diagnostiques mais il n'est pas la solution pratique. Il faut un équivalent pratique pour savoir comment régler un appareil entre sensibilité et spécificité en fonction de chaque valeur prise par la probabilité a priori ou prévalence. Cet équivalent pratique s'appelle la  qui est à l'origine la spécialité des radaristes. Elle est très rapide à obtenir sur un radar en tournant les boutons de volume en présence de cibles connues mais il en va tout autrement en biologie. En toxicologie, en biologie ou plus largement en médecine, il faudrait effectuer une mesure des fréquences diagnostiques observées pour chaque couple sensibilité-spécificité en fonction des valeurs prises par la probabilité a priori. En-dehors d'un travail de recherche particulièrement long et isolé, c'est difficilement réalisable à l'échelle de toutes les molécules à détecter une par une ou de tous les signes à prendre en compte un par un dans toutes les situations de prévalence. En l'absence de courbes ROC, on en reste toujours au résultat fourni par le théorème Bayes qui est largement suffisant en pratique quotidienne pour l'interprétation des résultats.

Puisque les courbes ROC en médecine ne sont pas établies, il faut, pour comparer deux résultats médicaux de même nature, que les opérateurs travaillent avec le même appareil réglé sur le même couple sensibilité-spécificité sur des personnes présentant le même signe. La prévalence est considérée comme établie à un moment donné et de ce point de vue non variable. Dans ces conditions, l'interprétation diagnostique faite entre deux médecins exécutant la même analyse séparément peut varier faiblement. C'est le but de la double lecture des mammographies dans le dépistage du cancer du sein.

La pathognomonie

Il existe un cas où l'interprétation diagnostique est univoque. C'est le cas où la sensibilité et la spécificité sont chacune égale à un ou 100%. Dans un tel cas, par définition, l'erreur diagnostique n'est pas possible et le résultat brut positif-négatif fait directement le diagnostic en le confirmant ou en le rejetant sans risque d'erreur. Il reste à savoir si un tel cas existe sachant qu'en biologie le risque d'erreur n'est jamais nul. Dans les analyses biologiques à résultat binaire ou quasi-binaire, on peut être tenté de considérer que le résultat est pathognomonique. Un résultat binaire est par exemple l'identification du chromosome X. C'est oui ou non. Par extension, on a voulu faire de la biologie cellulaire et des empreintes génétiques des analyses pathognomoniques. On sait aujourd'hui que l'interprétation diagnostique dans ce domaine est soumise à l'implacabilité du théorème de Bayes et que les erreurs tenant au contexte c'est à dire à la probabilité a priori sont statistiquement prévisibles. Dans les empreintes génétiques, le nombre de loci à comparer a été très logiquement augmenté de trois à cinq puis à huit. On s'était rendu compte aux Etats-Unis que le pourcentage d'erreurs pouvait être de 2% lors de contrôles de qualité externes dans certains laboratoires. Un pourcentage très éloigné de la sensibilité et de la spécificité qui peuvent atteindre un millionième.

VPP = probabilité d'avoir consommé le produit recherché quand le résultat biologique est positif.

VPN = probabilité de n'avoir pas consommé le produit recherché quand le résultat biologique est négatif.

HISTORIQUE DE LA DEMONSTRATION

EN DIAPORAMA

Les ressources indispensables

Pour introduire le sujet :

                      Diagnostics difficiles en médecine interne par Hugues Rousset, Denis Vital Durand,

                     Jean-Louis Dupond, et Michel Pavic (et les deux éditions antérieures)

Pour comprendre en français sur Wikipedia le théorème de Bayes et ses conséquences avant de se reporter aux sites en anglais :

http://fr.wikipedia.org/wiki/Théorème_de_Bayes

Pour comprendre en anglais sur Wikipedia les valeurs prédictives :

http://en.wikipedia.org/wiki/Positive_predictive_value

Pour approfondir en anglais sur Wikipedia les courbes ROC :

http://en.wikipedia.org/wiki/Receiver_operating_characteristic