Non-linéarité
LA NON-LINÉARITÉ
dans lequel on peut aisément remplacer x, y, z par des quantités Q1, Q2, Q3 ou des concentrations C1, C2, C3 dans un système de distribution pharmacocinétique à trois compartiments. La réponse est irrégulière, prédictible ou imprédictible à chaque nouvelle impulsion autrement dit chaotique au sens de la donc quand même déterministe. Avec des conditions initiales particulières, il est possible d'obtenir une réponse prédictible, stationnaire ou périodique, mais qui ne ressemble à rien de connu dans le monde linéaire.
Définition
On définit comme non linéaire un phénomène dont la réponse n'est pas proportionnelle à sa cause. Si la concentration d'une substance dans l'organisme à tout moment n'est pas strictement proportionnelle à la dose administrée, la cinétique de cette substance n'est pas linéaire. C'est le cas général. Toutefois, pour des questions de sécurité évidentes, les médicaments au comportement non linéaire dans l'organisme ont tendance à être remplacés dès qu'il en existe un autre aux mêmes effets dont la cinétique est linéaire et donc mieux contrôlable. Mais, même en procédant ainsi, les choses ne sont pas aussi simples. Car, il peut exister des effets linéaires avec une concentration non linéaire et, inversement, une concentration linéaire avec des effets non linéaires. Les médicaments avec la meilleure sécurité sont ceux qui ont une concentration linéaire et des effets désirés linéaires sans effet indésirable avec une toxicité faible. Ces contraintes reviennent très cher dans la recherche et le développement d'un médicament mais c'est à ce prix qu'on passe d'une médecine des plantes rudimentaire à une médecine pharmaceutique très souvent efficace dans plus de deux tiers des cas.
Systématisation
La non-linéarité est mais pour l'instant non exploitable. En revanche, elle permet de comprendre ce qui se passe quand rien ne marche. Pour décrire un phénomène non linéaire, il n'y a pas d'autre moyen pour l'instant que d'utiliser les équations différentielles. Il n'y a aucune perception intuitive possible du phénomène. Le nombre des comportements non linéaires est illimité et les formats d'expression le sont aussi.
Application à la pharmacocinétique
On peut retenir que la non-linéarité est la règle dans l'univers ce qui signifie en pharmacocinétique que les molécules en tout genre ont plus de chance d'avoir un comportement non linéaire que linéaire. Même si on réussit à ne retenir à la longue que des médicaments avec un comportement plus ou moins linéaire, les occasions de non-linéarité spontanées ou passagères dans une cinétique linéaire sont multiples. Elles peuvent dépendre notamment par exemple de la nature des médicaments, des moments où l'organisme subit leur intrusion, de l'état préalable de l'organisme, de la ligne de base et des méthodes de dosage.
Pour la nature des médicaments c'est évident. Le moment où l'organisme subit leur intrusion peut être le jour ou la nuit, l'exposition au soleil ou au contraire l'exposition au froid, le stress etc. L'état préalable de l'organisme est aussi bien le jeune âge, la vieillesse, l'exercice sportif intensif, une maladie, une imprégnation hormonale etc. La ligne de base concerne l'appareil de dosage et les conditions d'acquisition des données. La méthode de dosage fait intervenir la soustraction ou l'addition d'une partie non spécifique dont on sait qu'elle est très peu prise en compte avec précision en médecine.
Exemples
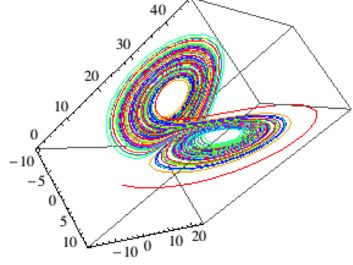
Les exemples de non-linéarité sont innombrables mais l'exemple plus fréquemment cité parce qu'il est historique donne un assez bon reflet de que pourrait être une pharmacocinétique non linéaire. Et, surtout, il rassemble toutes les particularités d'un système non linéaire: points fixes, points périodiques, attracteurs et attracteurs étranges. C'est le système de Lorenz (1963) où trois paramètres σ, r, b sont à considérer en valeurs initiales au même titre que x,y,z :
Les ressources indispensables
Pour introduire le sujet de la non-linéarité:
Nonlinear Dynamics And Chaos: With Applications To Physics, Biology, Chemistry, And Engineering
(Studies in nonlinearity) by Steven H. Strogatz (2001)by Steven H. Strogatz (2001)
et :
Pour comprendre de quoi il s'agit :
Le Que-sais-je de François Lurçat
ainsi que :
Un texte de David Aubin et bien d'autres
Pour approfondir :
Sans compter, pour résumer, une très utile suite de présentations des principaux systèmes chaotiques et leur contrôle de :
Une partie de l'exploitation mathématique avec Mathematica® au format html peut être consultée . Les possesseurs de Mathematica® pourront faire varier les conditions initiales et les paramètres σ, r, b pour faire apparaître et disparaître les points fixes, les points périodiques ou les attracteurs et observer qu'il s'agit d'un système chaotique déterministe.
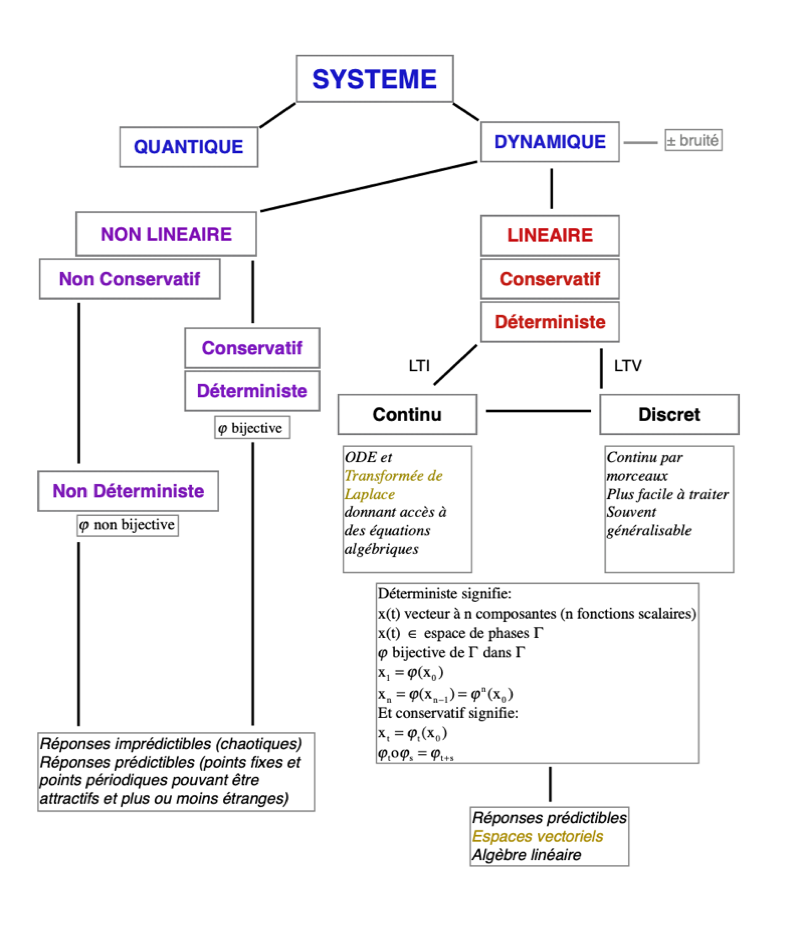
La classification des systèmes
Il est très facile de comprendre la classification des systèmes car ils sont très peu nombreux. En pharmacocinétique, on travaille toujours avec des systèmes linéaires. Ca ne signifie pas que tous les autres n'existent pas mais qu'il est plus facile de travailler pour des raisons de sécurité d'utilisation en médecine avec des médicaments qui ont un comportement linéaire. Il faut retenir que c'est une petite partie des comportements possibles dans l'univers de la biologie. Au sommet, il y a les systèmes probabilistes ou quantiques et les systèmes non probabilistes ou classiques ou dynamiques. Parmi les systèmes dynamiques, il y a les systèmes linéaires et les systèmes non linéaires. Parmi les systèmes linéaires, il y a les systèmes discrets ou continus par morceaux et les systèmes continus totalement. Parmi les systèmes non linéaires, il y a les systèmes bijectifs dont on peut prédire l'avenir et reconstituer le passé et les systèmes non bijectifs dont on peut prédire l'avenir mais pas reconstituer le passé du fait qu'une bijection n'a pas d'inverse.
Donc, on peut dire pour simplifier que les modèles les plus étudiés sont conservatifs et déterministes qu'ils soient linéaires ou non linéaires et qu'ils sont dynamiques c'est à dire non probabilistes. Mais aucun n'est à exclure et tous sont possibles à tout moment.
La différence entre tous les systèmes se trouve dans la précision des mesures. Il est toujours possible de négliger une ou plusieurs contributions à l'élaboration d'un système pour se retrouver le plus souvent possible dans l'intervalle continu d'un système dynamique linéaire. Mais, par moment, un système aussi simple peut échapper à sa description par l'intervention d'un mécanisme sous-jacent devenu prépondérant ou non négligeable. Un système n'est figé qu'autant que sont fixées toutes les conditions de son état dans un intervalle de temps.
Pour une revue de détail de l'élaboration et du choix du meilleur système, il est opportun de se rapporter au texte de la de David Ruelle. Un système peut échapper à tout moment à toute prévision. L'imprécision sur la mesure de l'état initial conditionne l'imprécision de la prévision sur l'état final. Pour un système linéaire c'est intuitif. Mais, pour un système non linéaire, l'imprécision sur l'état initial peut rendre impossible toute prévision sur l'état final. Cet échappement a été formalisé par Lyapunov. Plus un système non linéaire est fortement chaotique moins l'état final est prévisible au point qu'il peut devenir totalement imprévisible quelle que soit l'état initial. La différence d'un système chaotique à l'autre dépend de l'horizon de Lyapunov qui est un temps caractéristique du système au-delà duquel l'imprécision devient exponentiellement non négligeable. D'où une extrême sensibilité aux conditions initiales qui est la définition d'un système chaotique.
Les transitions entre systèmes
La question est encore aujourd'hui de savoir si un système biologique donné est définitivement linéaire ou non linéaire et ce par morceaux bien évidemment. En pharmacologie, la question a été partiellement résolue puisqu'on sait que les paramètres pharmacocinétiques linéaires peuvent varier en fonction de la gravité de l'état d'une maladie (voir R.W. Jelliffe). Si la linéarité peut varier, le passage de la linéarité à la non-linéarité est forcément possible aussi. D'un point de vue mathématique, il existe pour l'heure de passage d'un système linéaire à un système non linéaire (les scénarios de Feigenbaum, de Ruelle-Takens et de Pomeau-Manneville) tout en restant dans un système chaotique donc déterministe et conservatif. Déterministe signifie qu'à une condition initiale correspondra un et un seul état à un instant ultérieur quelconque et qu'on pourra reconstituer un état antérieur à partir d'un état ultérieur. Conservatif signifie que tout état est une condition initiale pour un état suivant. Les aller-retours incessants de la théorie à la pratique permettront de mettre au jour de nombreuses variétés de systèmes biologiques en correspondance avec une modélisation mathématique et inversement de mettre une modélisation mathématique en face d'un système biologique. On croit toujours que les mathématiques précèdent la nature alors qu'en fait dans l'étude des systèmes elles courent après la nature.

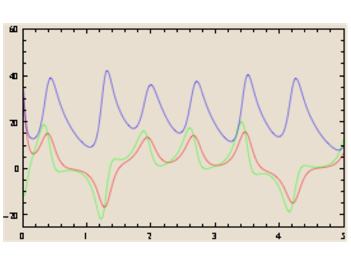
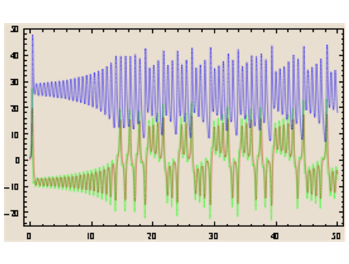
Chaque impulsion ou prise de médicament peut donner une répartition irrégulière
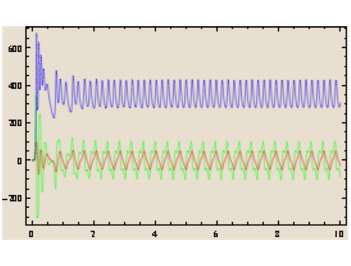
La prise de médicament suivante
donne une autre réponse
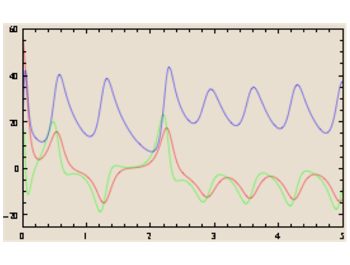
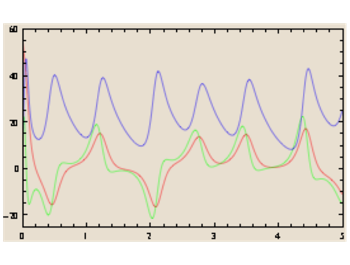
Et ainsi de suite
Au total, à chaque prise de médicament, le résultat est irrégulier mais prévisible et, à chaque modification de σ, r, b, il devient différent et peut devenir imprévisible
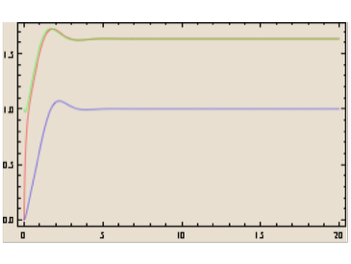
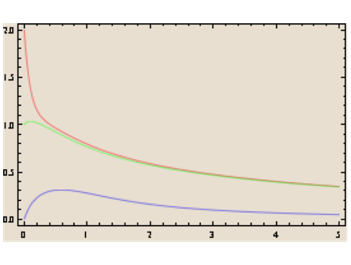
Dans certaines conditions, un état stationnaire peut apparaître et le médicament ne serait pas éliminé
Dans d'autres conditions, apparaît un état stationnaire convergeant vers zéro qui ressemble étonnamment à un système linéaire à trois compartiments en pharmacocinétique classique
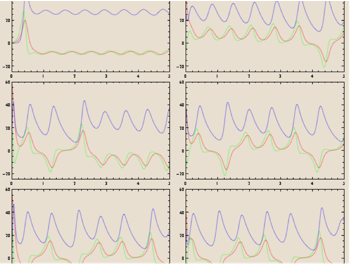
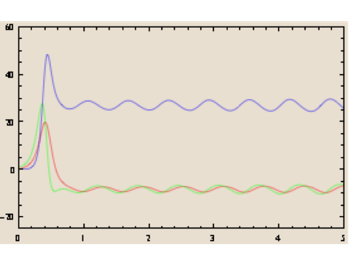
Le système peut évoluer
vers un état pseudo-périodique
ou un état périodique
ou un autre état périodique
et bien sûr l'attracteur étrange