Le périmètre

On est bien d'accord qu'en médecine la seule adaptation de posologie massivement souhaitée est celle qui recommande un, deux ou trois comprimés par jour pendant la durée nécessaire. Tous les efforts de l'industrie pharmaceutique vont dans ce sens et ce schéma très simple sera toujours le plus recherché. Mais, dans un certain nombre de situations, il faut pouvoir recourir à une adaptation de posologie plus élaborée, informatisée et individualisée. Ces rares cas imposent quelques impératifs. Il faut un médicament dont le potentiel toxique est élevé, dont la concentration et les effets désirés sont très bien corrélés, dont la concentration et les effets sont linéaires, dont la distribution se limite à un ou deux compartiments et enfin pour lesquels il existe une cible de concentration thérapeutique bien établie au moins pour initier le schéma thérapeutique.

L'adaptation de posologie informatisée et individualisée conjugue linéarité, sous-population, mathématiques et informatique. C'est la raison pour laquelle elle est la forme la plus aboutie de l'étude et de l'usage de la pharmacocinétique d'un médicament. Mais, ce niveau d'élaboration peut a contrario être un facteur limitant de son étude et de sa diffusion.

La référence

L'adaptation de posologie informatisée et individualisée mise au point par la faculté de médecine de  l'université de Californie du Sud est d'une très grande précision et elle est parfaitement réalisable en routine dans un service hospitalier qui bénéficie d'un fort recrutement de pathologies homogènes. La partie la plus longue est la mise en place qui précède le passage en routine. Sa mise en place nécessite un biologiste formé à la pharmacocinétique qui définira les sous-populations à traiter, recueillera les paramètres des méthodes de dosage, établira les paramètres pharmacocinétiques dits de population de ces sous-populations, maîtrisera les logiciels BestDose et Pmetrics initialement appelés USC-pack dédiés à cette tâche, exigera une mention des temps en heures, minutes et secondes pour les prélèvements et les administrations de médicament, recueillera les quelques paramètres biologiques indispensables comme le poids, la taille, le sexe, la clairance à la créatinine ou la créatininémie puis qui réalisera l'adaptation de posologie en trente à soixante minutes à compter du moment où les concentrations sanguines lui sont communiquées. Il faut un personnel volontaire, méthodique et précis. L'adaptation de posologie informatisée et individualisée ne peut pas s'accommoder d'approximations dans la mesure où la méthode repose lors sa mise au point mathématique sur la minimisation de toutes les erreurs de toute origine.

La routine

L'utilisation du logiciel en routine consiste uniquement à déterminer, pour un patient donné, un volume de distribution et une constante d'élimination dans un modèle à un compartiment plus deux constantes d'échange entre les deux compartiments dans un modèle à deux compartiments. Il est intéressant de noter que ces paramètres individuels peuvent éventuellement varier au cours de la maladie en cas de très nette aggravation ou de très nette amélioration mais le modèle mathématique étant linéaire il n'y a aucun obstacle logiciel à la poursuite de l'adaptation puisqu'il est toujours possible de repartir du dernier cycle en ne tenant compte que de la dernière condition initiale.

La simplification française

L'apport théorique le plus important à l'adaptation de posologie a été fourni par un français Alain Mallet qui a démontré que les paramètres pharmacocinétiques d'une sous-population pouvaient se réduire à un nombre fini de valeurs. Cette démonstration a fait de la pharmacocinétique un sujet nettement moins abstrait qu'une infinie variété de courbes de densité de probabilité qui s'entrecroisent et se chevauchent. Et, surtout elle permet de schématiser l'application du théorème de Bayes qui se comprend toujours mieux avec des ensembles finis de valeurs finies.

L'historique

En revanche, l'historique qui a permis d'arriver à la forme d'adaptation de posologie informatisée et individualisée connue de nos jours peut paraître infiniment complexe.

Poser le problème en quatre figures

Dans sa forme la plus élaborée, il faut retenir que l'adaptation de posologie est posée en termes bayésiens. Ensuite, c'est les ordinateurs qui permettront ou non d'effectuer des calculs réellement bayésiens ou partiellement bayésiens ou inspirés du calcul bayésien. Le problème est donc: Etant donné une sous-population dont les individus portent chacun des valeurs caractéristiques des paramètres pharmacocinétiques comme la clairance Cl et le volume de distribution V et étant donné un résultat obtenu sur un individu i fait de valeurs démographiques z et biologiques y dont une ou plusieurs mesures par exemple de la concentration C(t), quelle est la valeur la plus probable de tel et tel paramètre pharmacocinétique pouvant le caractériser sachant que les valeurs prises par les paramètres pharmacocinétiques sont en nombre fini ?

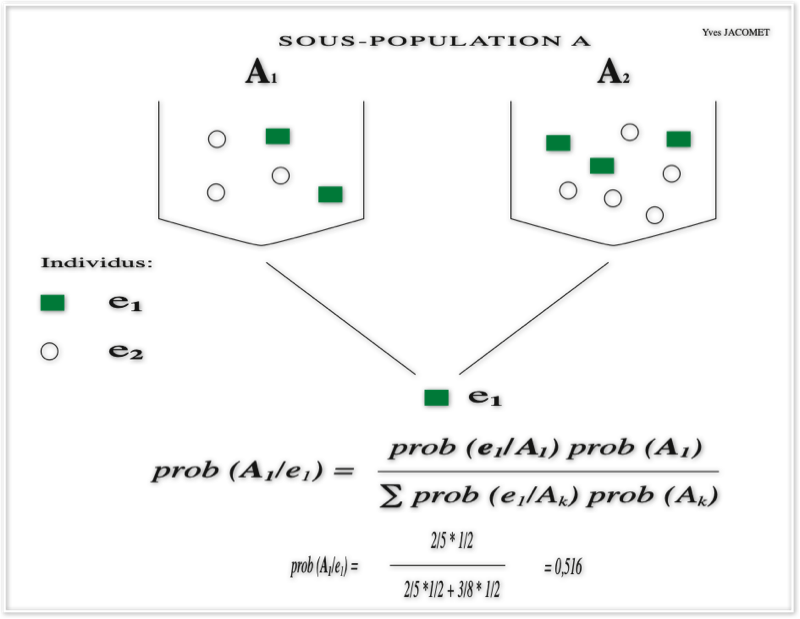
Sur la première figure, on pose le théorème de Bayes de manière absolument classique: à partir du résultat ou événement e d'un individu i, à quelle urne appartient-il parmi deux urnes exclusives l'une de l'autre formant ensemble la sous-population A ?

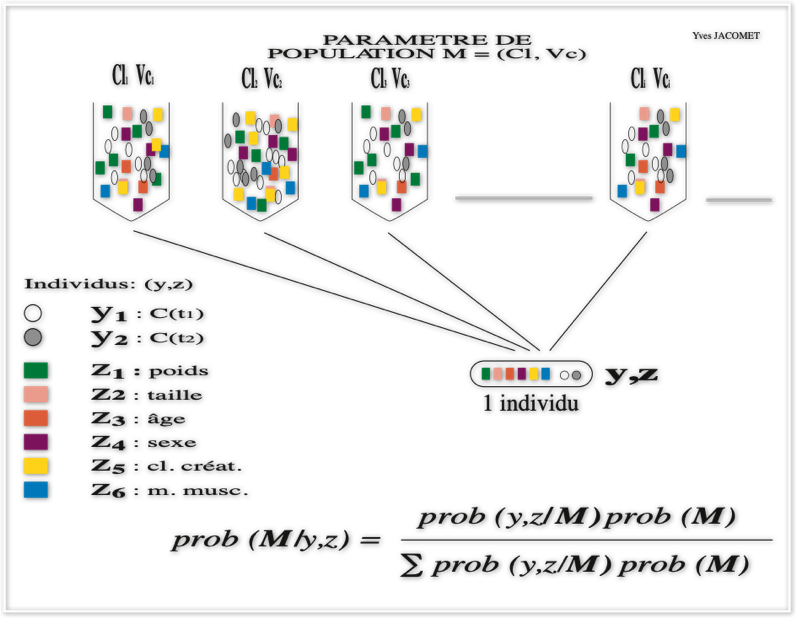
Sur la quatrième figure, on récapitule les paramètres pharmacocinétiques pris en considération en fonction du modèle compartimental de départ; ils s'expriment comme un vecteur de paramètres appartenant à l'espace d'état ou espace des phases qui est l'ensemble des variables dynamiques du système. Quand la calcul est mené sans considération de la forme de la densité de probabilité des paramètres pharmacocinétiques, on dit que le calcul est non paramétrique au sens statistique du terme c'est à dire que la moyenne et la variance calculées ne sont par exemple pas celles d'une courbe de Gauss.

Au terme de cette démonstration, on n'oublie pas que la difficulté de l'adaptation de posologie et disons même les erreurs repose sur le fait qu'un patient peut changer à tout moment de paramètre M, de sous-population A ou passer d'un système linéaire à un système non linéaire. Les recommandations d'une adaptation de posologie sont donc faites toute chose étant égale par ailleurs. On est à peu près certain que l'adaptation de posologie informatisée et individualisée prédira parfaitement bien, on dit de manière raisonnable, les valeurs de concentration attendues à condition que les conditions initiales soient connues avec un minimum d'approximation et que le modèle sous-jacent retenu ne change pas entre-temps. C'est heureusement ce qu'on observe dans l'immense majorité des cas mais comme toujours il est impossible de certifier le résultat à l'avance dans 100% des cas.

Au total

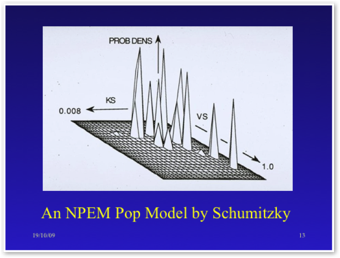
L'adaptation de posologie peut se faire de manière classique dite paramétrique à partir de paramètres pharmacocinétiques obtenus en calculant leurs moyennes et leurs écarts-types associés à une courbe d'erreur de la mesure expérimentale en fonction des méthodes de dosage utilisées. C'est la méthode la plus répandue et la plus rapide qui recourt à la traditionnelle régression non linéaire par minimisation des carrés des écarts. Mais, une véritable adaptation de posologie bayésienne doit se faire sur l'éventail des valeurs en nombre fini des paramètres pharmacocinétiques obtenus par la méthode ci-dessus dite non paramétrique ou NPEM de Schumitzky applicable aux distributions de probabilité discrètes (1991). Ci-dessous, les deux illustrations de R.W. Jelliffe :

Dès lors, chaque patient fait l'objet d'une adaptation posologique à la valeur du paramètre le plus proche au lieu d'une adaptation à la valeur moyenne de tous les paramètres.

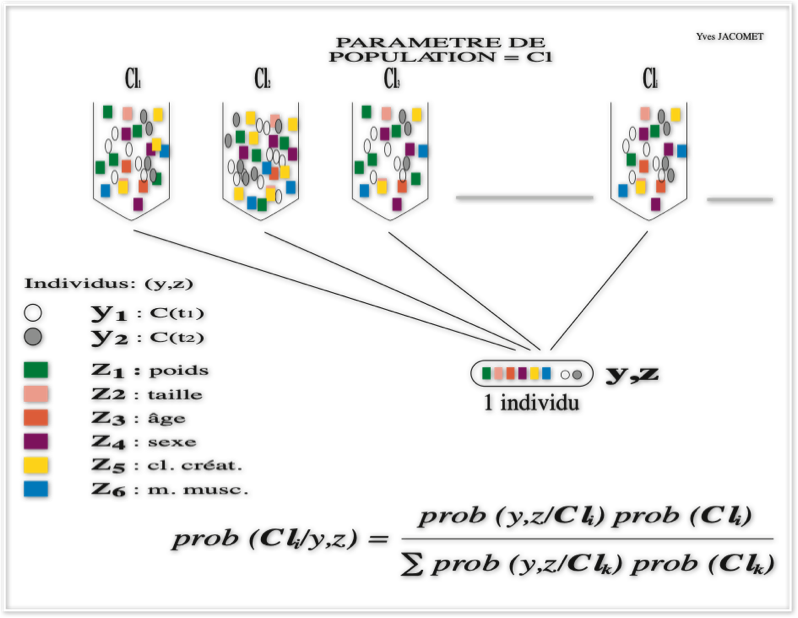
Sur la deuxième figure, on généralise le théorème de Bayes à plusieurs urnes en nombre fini exclusives les unes des autres pour le premier paramètre pharmacocinétique, e.g. la clairance Cl, formant ensemble la sous-population étudiée et on pose la question rituelle: Etant donné un ensemble de valeurs démographiques et biologiques recueilli sur un individu issu de la sous-population étudiée, à quelle urne de la valeur de clairance la plus vraisemblable appartient-il ?

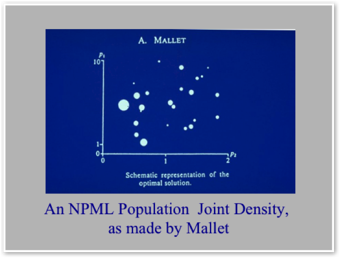
Une autre présentation entièrement équivalente est celle de Alain Mallet (NPML,1986) qui est le découvreur de la méthode non paramétrique toujours cité comme tel par l'équipe de R.W. Jelliffe :

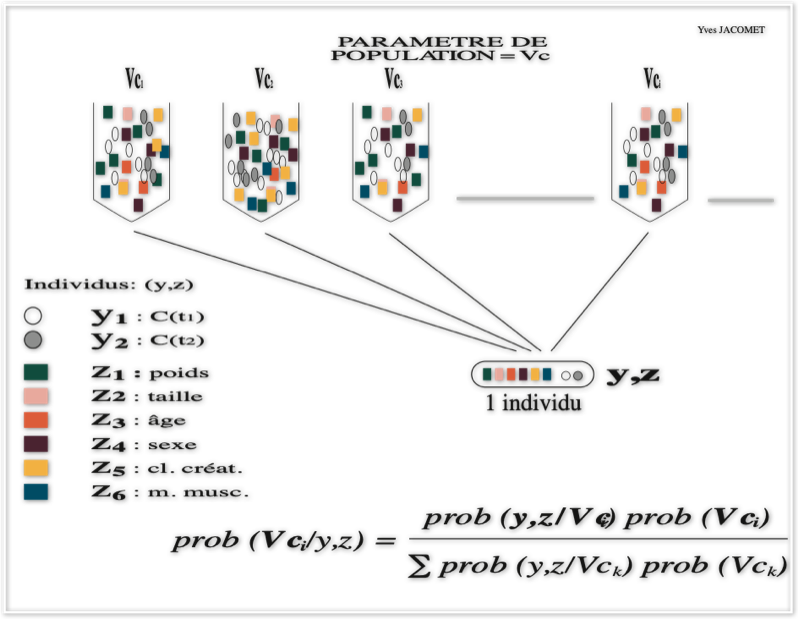
Sur la troisième figure, idem, on généralise le théorème de Bayes à plusieurs urnes en nombre fini exclusives les unes des autres pour le deuxième paramètre pharmacocinétique, e.g. le volume central de distribution Vc, formant ensemble la même sous-population étudiée et on pose le même type de question: Etant donné un ensemble de valeurs démographiques et biologiques recueilli sur le même individu issu de la sous-population étudiée, à quelle urne de la valeur du volume central de distribution la plus vraisemblable appartient-il ?